Ever wondered why flowers often have similar numbers of petals? When I am demonstrating flower making at Coalport china Museum I am often asked about the number of petals I use. The flower I was first taught were a set number. As I have developed my own flowers I have sort of fell into a set number of petals on each row. I must be in tune with nature as these numbers are taken from nature and they have a name, Fibonacci Numbers.
The Fibonacci sequence goes like this:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …..
The next number is found by adding up the two numbers before it:
0+1=1, 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5= 13, 13+8=21 and so on
My rose flowers for instance, the very first flower I was taught was the 5 petal rose. It has 1 centre section, 2 petals around the center, then 3 petals around that. Then I moved on to the 8 petal rose. One center, 3 petals around that, then five around that. See the 8 petal rose below, and the Anemone which is a set 5 petal flower.


Now I have developed the rose further for larger roses and the rows of petals always fall into these numbers below. It just always looks more aesthetically pleasing. If you count the rows of petals on my Angel Rose you can see the first row has 2, then 3, then 5, then 8. It just looks best when using these numbers.
Interesting as you go to higher numbers in the sequence, the ratio of two successive numbers approaches the golden ratio.
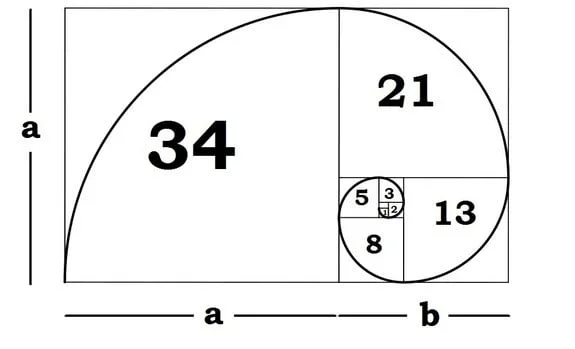
The golden ratio is a special number found by dividing a line into two parts so that the longer part divided by the smaller part is also equal to the whole length divided by the longer part.
As an equation it looks like this:
a/b = (a+b)/a = 1.6180339887498948420
As with pi (the ratio of the circumference of a circle to its diameter), the digits go on and on, theoretically into infinity. Phi is usually rounded off to 1.618 and this is a common number throughout nature.
The numbers of petals in many flowers (not all) follow the Fibonacci sequence. Oddly Phi appears as each petal is placed at 0.618034 per turn (out of a 360° circle) which is allowing for the best possible exposure to sunlight.
The golden ratio is found in all sorts of nature including shells, flowers, trees, faces, hurricanes, animals, and even spiral galaxies!
It has also been used by artists and architects, including Le Corbusier and Dalí. They proportioned their work to approximate the golden ratio as they believed it was aesthetically pleasing. There is talk on whoever built the Great Pyramids of Egypt used these foundations of mathematics and geometry. And it can also be found in great music. Some of Mozarts famous sonatas use this golden number. The golden ratio appears in the relationship of the intervals or distance between the notes.
Examples of Flowers using the Fibonacci Numbers
- Lilies and Iris have 3 petals
- Buttercups and Pinks have 5 petals
- Some delphinium have 5 petals
- The Marigold has 13 petals
- Some Asters have 21
- Daisy can often be found with 21, 34, 55 and 89
- The Black-eyed Susan has 21 petals
Sunflowers grow patterns of seeds in a spiral shape. The spiral happens naturally because each new cell is formed after a turn.

There are plenty of examples in the food we eat, pineapples, artichokes, and pine cones, apples, bananas, lettuce, cauliflower, Broccoli, the list goes on.
Nature is truly mind-blowing, and how maths and science can be entwined. I have long been facincated with nature and physics. This golden ratio is even found in Quantum Physics. I have been studying Quantum Physics for a while now. You can read about how the golden ratio has been discovered in the quantum world here.
I intend to always consciously try to use these numbers on my sculptures. Not sure I can manage the sunflower centre mind you, but roses and general flowers I will. They don’t look right if I don’t follow the sequence. So if these numbers are good enough to use by the greats like Dali (always been a fan) then it’s good enough for the Mother of Flower People!
